第 9 章 调度：比例份额 ¶

彩票调度 (lottery scheduling)

每隔一段时间，都会举行一次彩票抽奖，以确定接下来应该运行哪个进程。越是应该频繁运行的进程，越是应该拥有更多地赢得彩票的机会。

9.1 基本概念：彩票数表示份额 ¶

彩票数 (ticket) 代表了进程（或用户或其他）占有某个资源的份额。一个进程拥有的彩票数占总彩票数的百分比，就是它占有资源的份额。

9.2 彩票机制 ¶

彩票货币 (ticket currency)

用户可以为他们的进程或任务分配“局部彩票”，而这些局部彩票随后会根据用户的总彩票配额被转换成“全局彩票”，以此允许用户以更灵活和细粒度的方式分配系统资源。

彩票转让 (ticket transfer)

进程可以将它持有的一部分或全部彩票转让给另一个进程，以便临时提高接收进程的调度优先级。在 客户端 / 服务端 模型的应用场景中，客户端请求服务端执行某项任务时，可以选择将一部分或者全部彩票转让给服务端，从而更快地完成客户端请求的任务。

彩票通胀 (ticket inflation)

进程可以临时提升或降低自己拥有的彩票数量，但在竞争环境中进程之间互相不信任，就没什么意义了。

9.3 实现 ¶

使用单向链表来记录所有的进程及其彩票数。

graph LR;
    HEAD --> A[Job: A, Tix: 100];
    A --> B[Job: B, Tix: 50];
    B --> C[Job: C, Tix: 50];
    C --> NULL

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// counter: used to track if we've found the winner yet
int counter = 0;

// winner: use some call to a random number generator to
// get a value, between 0 and the total # of tickets
int winner = getrandom(0, totaltickets);

// current: use this to walk through the list of jobs
node_t *current = head;

// loop until the sum of ticket values is > the winner
while (current) {
  counter = counter + current->tickets;
  if (counter > winner)
  break; // found the winner
  current = current->next;
}
// 'current' is the winner: schedule it...

从前向后遍历链表，将每张票的值加到 counter 上，直到超过 winner，此时的节点对应进程就是中奖者。

要让这个过程更有效率，可以保持链表递减排序，这样就能使用最小的迭代次数找到需要的节点。（并不会影响算法正确性，机率只于彩票数有关，与顺序无关）

9.4 一个例子 ¶

假设两个相互竞争的工作，每个工作都有相同数目的 100 张彩票，以及相同的运行时间 \(R\)。

我们希望两个工作在大约同时完成，但由于彩票调度算法的随机性，有时一个工作会先于另一个完成。为了量化这种区别，我们定义了一个简单的不公平指标 \(U\) (unfairness metric)，将两个工作完成时刻相除得到 \(U\) 的值。

比如运行时间 \(R\) 为 10，第一个工作在时刻 10 完成，另一个在 20，\(U = \frac{10}{20} = 0.5\)。

如果两个工作几乎同时完成，\(U\) 的值将很接近于 1。

在这种情况下，我们的目标是：完美的公平调度程序可以做到 \(U = 1\)。

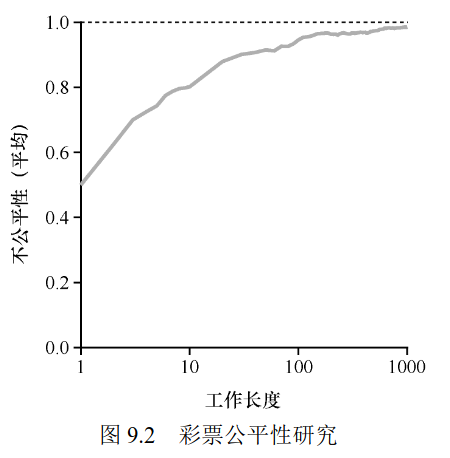
图中展示了两个工作的运行时间从 1 到 1000 变化时，30 次实验的平均 \(U\) 值。

可以看出，当工作执行时间很短时，平均不公平度非常糟糕。只有当工作执行非常多的时间片时，彩票调度算法才能得到期望的结果。

这个很符合“抛硬币”的直觉对吧，抛的次数越多，概率就越趋近于二分之一。

9.5 如何分配彩票 ¶

就算用户知道如何分配，也只能表示个大概，没有办法指定一个确切的策略，因为用户也没法确切地“知道”。

我是这么理解的。

9.6 为什么是不确定的 ¶

在示例中，3 个进程 (A, B, C) 的步长值分别为 100、200 和 40，初始行程值都为 0。

1. 最初所有的进程都可能被选择执行，假设选择 A，执行一个时间片之后，更新行程值为 100
2. 运行 B，更新行程值为 200
3. 执行 C，更新行程值为 40
4. 最小还是 C，执行并增加行程值到 80
5. 最小仍是 C，执行并增加行程值到 120
6. 运行 A，更新行程值为 200（于 B 相同）
7. C，更新行程值为 160
8. C，更新行程值为 200

C 运行了 5 次，A 运行了 2 次，B 一次，正好是票数的比例———— 200、100 和 50。

彩票调度算法只能一段时间后，在概率上实现比例，而步长调度算法可以在每个调度周期后做到完全正确。

但是彩票调度有一个步长调度没有的优势————不需要全局状态。

一个新的进程在执行过程中加入系统，应该怎么设置行程值？设置成 0 的话就独占 CPU 了。

彩票算法只需要用新进程的票数更新全局的总票数就可以了，因为彩票调度算法能够更合理地处理新加入的进程。

9.7 小结 ¶

彩票调度和步长调度都没能作为 CPU 调度被广泛使用，一个原因是 都不能很好地适合 I/O，另一个原因是 其中最难的票数分配问题没有确定的解决方式。

作业 ¶

$ ./lottery.py -j 3 -s 1 -c
$ ./lottery.py -j 3 -s 2 -c
$ ./lottery.py -j 3 -s 3 -c

$ ./lottery.py -l 10:1,10:100 -c

$ # U = 196 / 200 = 0.98
$ ./lottery.py -l 100:100,100:100 -s 1 -c | grep DONE
--> JOB 1 DONE at time 196
--> JOB 0 DONE at time 200

$ # U = 190 / 200 = 0.95
$ ./lottery.py -l 100:100,100:100 -s 2 -c | grep DONE
--> JOB 1 DONE at time 190
--> JOB 0 DONE at time 200

$ # U = 181 / 200 = 0.905
$ ./lottery.py -l 100:100,100:100 -s 5 -c | grep DONE
--> JOB 1 DONE at time 181
--> JOB 0 DONE at time 200